Recent Publications, Papers, and News
Machine Learning Global Simulation of Nonlocal Gravity Wave Propagation
Authors:
Aman Gupta, Aditi Sheshadri, Sujit Roy, Vishal Gaur, Manil Maskey, and Rahul Ramachandran
Abstract:
Global climate models typically operate at a grid resolution of hundreds of kilometers and fail to resolve atmospheric mesoscale processes, e.g., clouds, precipitation, and gravity waves (GWs). Model representation of these processes and their sources is essential to the global circulation and planetary energy budget, but subgrid scale contributions from these processes are often only approximately represented in models using parameterizations. These parameterizations are subject to approximations and idealizations, which limit their capability and accuracy.
Regression Forest Approaches to Gravity Wave Parameterization for Climate Projection
Authors:
David S. Connelly and Edwin P. Gerber
Abstract:
We train random and boosted forests, two machine learning architectures based on regression trees, to emulate a physics-based parameterization of atmospheric gravity wave momentum transport. We compare the forests to a neural network benchmark, evaluating both offline errors and online performance when coupled to an atmospheric model under the present day climate and in 800 and 1,200 ppm CO2 global warming scenarios. Offline, the boosted forest exhibits similar skill to the neural network, while the random forest scores significantly lower. Both forest models couple stably to the atmospheric model, and control climate integrations with the boosted forest exhibit lower biases than those with the neural network.
Gravity Wave Momentum Fluxes from 1 km Global ECMWF Integrated Forecast System
Authors:
Aman Gupta, Aditi Sheshadri, and Valentine Anantharaj
Abstract:
Progress in understanding the impact of mesoscale variability, including gravity waves (GWs), on atmospheric circulation is often limited by the availability of global fine-resolution observations and simulated data. This study presents momentum fluxes due to atmospheric GWs extracted from four months of an experimental “nature run", integrated at a 1 km resolution (XNR1K) using the Integrated Forecast System (IFS) model. Helmholtz decomposition is used to compute zonal and meridional flux of vertical momentum from ~1.5 petabytes of data; quantities often emulated by climate model parameterization of GWs.
Insights on Lateral Gravity Wave Propagation in the Extratropical Stratosphere From 44 Years of ERA5 Data
Authors:
Aman Gupta, Aditi Sheshadri, M. Joan Alexander, and Thomas Birner
Abstract:
The study presents (a) a 44-year wintertime climatology of resolved gravity wave (GW) fluxes and forcing in the extratropical stratosphere using ERA5, and (b) their composite evolution around gradual (final warming) and abrupt (sudden warming) transitions in the wintertime circulation, focusing on lateral fluxes. The transformed Eulerian mean equations are leveraged to provide a glimpse of the importance of GW lateral propagation (i.e., horizontal propagation) toward driving the wintertime stratospheric circulation by analyzing the relative contribution of the vertical versus meridional flux dissipation.
The impact of transience in the interaction between orographic gravity waves and mean flow
Authors:
Felix Jochum, Ray Chew, François Lott, Georg S. Voelker, Jan Weinkaemmerer, and Ulrich Achatz
Abstract:
A Lagrangian gravity-wave parameterization (MS-GWaM, Multi-Scale Gravity-Wave Model) that allows for fully transient wave-mean-flow interaction and horizontal propagation is applied to orographic gravity waves for the first time. Both linear and nonlinear mountain waves are modeled in idealized simulations within the pseudo-incompressible flow solver PincFlow. Two-dimensional flows over monochromatic orographies are considered, using MS-GWaM either in its fully transient implementation or in a steady-state implementation that represents classic mountain-wave parameterizations. Comparisons of wave-resolving simulations (not using MS-GWaM) and coarse-resolution simulations (using MS-GWaM) show that allowing for transience leads to a significantly more accurate forcing of the resolved mean flow.
A Constrained Spectral Approximation of Subgrid-Scale Orography on Unstructured Grids
Authors:
Ray Chew, Stamen Dolaptchiev, Maja-Sophie Wedel, and Ulrich Achatz
Abstract:
The representation of subgrid-scale orography is a challenge in the physical parameterization of orographic gravity-wave sources in weather forecasting. A significant hurdle is encoding as much physical information with as simple a representation as possible. Other issues include scale awareness, that is, the orographic representation has to change according to the grid cell size and usability on unstructured geodesic grids with non-quadrilateral grid cells. This work introduces a novel spectral analysis method approximating a scale-aware spectrum of subgrid-scale orography on unstructured geodesic grids.
Data Imbalance, Uncertainty Quantification, and Transfer Learning in Data-Driven Parameterizations: Lessons From the Emulation of Gravity Wave Momentum Transport in WACCM
Authors:
Qiang Sun, Hamid Pahlavan, Ashesh Chattopadhyay,Pedram Hassanzadeh, Sandro Lubis, M. Joan Alexander, Edwin Gerber, Aditi Sheshadri, and Yifei Guan
Abstract:
Neural networks (NNs) are increasingly used for data-driven subgrid-scale parameterizations in weather and climate models. While NNs are powerful tools for learning complex non-linear relationships from data, there are several challenges in using them for parameterizations. Three of these challenges are (a) data imbalance related to learning rare, often large-amplitude, samples; (b) uncertainty quantification (UQ) of the predictions to provide an accuracy indicator; and (c) generalization to other climates, for example, those with different radiative forcings. Here, we examine the performance of methods for addressing these challenges using NN-based emulators of the Whole Atmosphere Community Climate Model (WACCM) physics-based gravity wave (GW) parameterizations as a test case.
Uncertainty Quantification of a Machine Learning Subgrid-Scale Parameterization for Atmospheric Gravity Waves
Authors:
Laura Mansfield and Aditi Sheshadri
Abstract:
Subgrid-scale processes, such as atmospheric gravity waves (GWs), play a pivotal role in shaping the Earth’s climate but cannot be explicitly resolved in climate models due to limitations on resolution. Instead, subgrid-scale parameterizations are used to capture their effects. Recently, machine learning (ML) has emerged as a promising approach to learn parameterizations. In this study, we explore uncertainties associated with a ML parameterization for atmospheric GWs.
On the importance of learning non-local dynamics for stable data-driven climate modeling: A 1D gravity wave-QBO testbed
Authors:
Hamid A. Pahlavan, Pedram Hassanzadeh, and M. Joan Alexander
Abstract:
Machine learning (ML) techniques, especially neural networks (NNs), have shown promise in learning subgrid-scale parameterizations for climate models. However, a major problem with data-driven parameterizations, particularly those learned with supervised algorithms, is model instability. Current remedies are often ad-hoc and lack a theoretical foundation. Here, we combine ML theory and climate physics to address a source of instability in NN-based parameterization. We demonstrate the importance of learning spatially non-local dynamics using a 1D model of the quasi-biennial oscillation (QBO) with gravity wave (GW) parameterization as a testbed. While common offline metrics fail to identify shortcomings in learning non-local dynamics, we show that the concept of receptive field (RF) can identify instability a-priori.
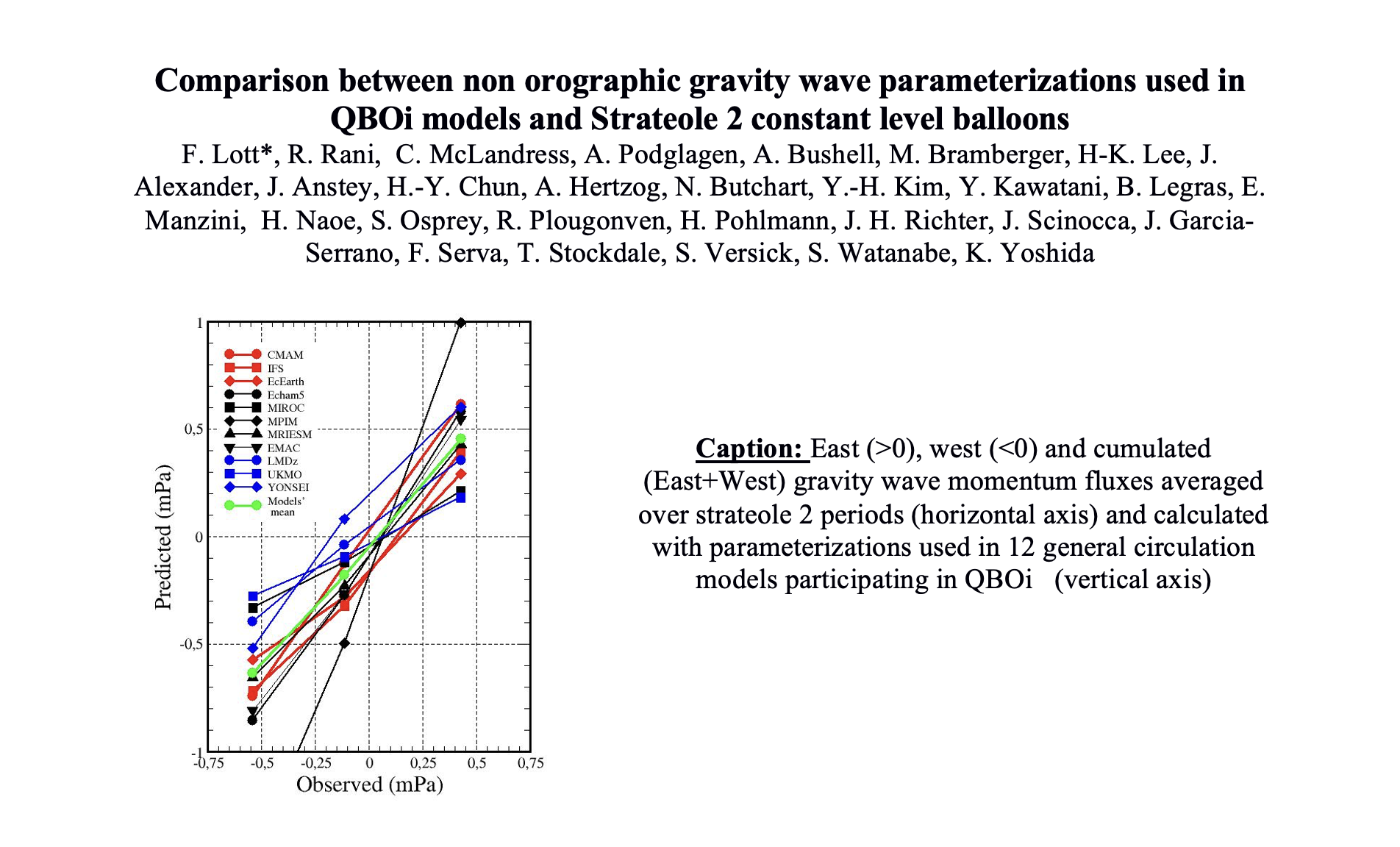
Comparison between non-orographic gravity-wave parameterizations used in QBOi models and Strateole 2 constant-level balloons
Authors:
F. Lott, R. Rani, C. McLandress, A. Podglajen, A. Bushell, M. Bramberger, H.-K. Lee, J. Alexander, J. Anstey, H.-Y. Chun, A. Hertzog, N. Butchart, Y.-H. Kim, Y. Kawatani, B. Legras, E. Manzini, H. Naoe, S. Osprey, R. Plougonven, H. Pohlmann, J. H. Richter, J. Scinocca, J. García-Serrano, F. Serva, T. Stockdale, S. Versick, S. Watanabe, K. Yoshida
Abstract:
Gravity-wave (GW) parameterizations from 12 general circulation models (GCMs) participating in the Quasi-Biennial Oscillation initiative (QBOi) are compared with Strateole 2 balloon observations made in the tropical lower stratosphere from November 2019–February 2020 (phase 1) and from October 2021–January 2022 (phase 2). The parameterizations employ the three standard techniques used in GCMs to represent subgrid-scale non-orographic GWs, namely the two globally spectral techniques developed by Warner and McIntyre (1999) and Hines (1997), as well as the “multiwaves” approaches following the work of Lindzen (1981).
Learning Closed-Form Equations for Subgrid-Scale Closures From High-Fidelity Data: Promises and Challenges
Authors:
Karan Jakhar, Yifei Guan, Rambod Mojgani, Ashesh Chattopadhyay, and Pedram Hassanzadeh
Abstract:
There is growing interest in discovering interpretable, closed-form equations for subgrid-scale (SGS) closures/parameterizations of complex processes in Earth systems. Here, we apply a common equation-discovery technique with expansive libraries to learn closures from filtered direct numerical simulations of 2D turbulence and Rayleigh-Bénard convection (RBC). Across common filters (e.g., Gaussian, box), we robustly discover closures of the same form for momentum and heat fluxes. These closures depend on nonlinear combinations of gradients of filtered variables, with constants that are independent of the fluid/flow properties and only depend on filter type/size. We show that these closures are the nonlinear gradient model (NGM), which is derivable analytically using Taylor-series.
MS-GWaM: A Three-Dimensional Transient Gravity Wave Parametrization for Atmospheric Models
Authors:
Georg S. Voelker, Gergely Bölöni, Young-Ha Kim, Günther Zängl, and Ulrich Achatz
Abstract:
Parameterizations for internal gravity waves in atmospheric models are traditionally subject to a number of simplifications. Most notably, they rely on both neglecting wave propagation and advection in the horizontal direction (single-column assumption) and an instantaneous balance in the vertical direction (steady-state assumption). While these simplifications are well justified to cover some essential dynamic effects and keep the computational effort small, it has been shown that both mechanisms are potentially significant. In particular, the recently introduced Multiscale Gravity Wave Model (MS-GWaM) successfully applied ray-tracing methods in a novel type of transient but columnar internal gravity wave parameterization (MS-GWaM-1D). We extend this concept to a three-dimensional version of the parameterization (MS-GWaM-3D) to simulate subgrid-scale nonorographic internal gravity waves.
Reconstructing Balloon-Observed Gravity Wave Momentum Fluxes Using Machine Learning and Input From ERA5
Authors:
Sothea Has, Riwal Plougonven, Aurélie Fischer, Raj Rani, Francois Lott, Albert Hertzog, Aurélien Podglajen, Milena Corcos
Abstract:
Global atmospheric models rely on parameterizations to capture the effects of gravity waves (GWs) on middle atmosphere circulation. As they propagate upwards from the troposphere, the momentum fluxes associated with these waves represent a crucial yet insufficiently constrained component. The present study employs three tree-based ensemble machine learning (ML) techniques to probe the relationship between large-scale flow and small-scale GWs within the tropical lower stratosphere.
Recreating Observed Convection-Generated Gravity Waves From Weather Radar Observations via a Neural Network and a Dynamical Atmospheric Model
Authors:
Christopher Kruse, J. Alexander, M. Bramberger, A. Chattopadhyay, P. Hassanzadeh, B. Green, A. Grimsdell, L. Hoffmann
Abstract:
Convection-generated gravity waves (CGWs) transport momentum and energy, and this momentum is a dominant driver of global features of Earth’s atmosphere’s general circulation (e.g., the quasi-biennial oscillation, the pole-to-pole mesospheric circulation). As CGWs are not generally resolved by global weather and climate models, their effects on the circulation need to be parameterized. However, quality observations of GWs are spatiotemporally sparse, limiting understanding and preventing constraints on parameterizations. Convection-permitting or -resolving simulations do generate CGWs, but validation is not possible as these simulations cannot reproduce the CGW-forcing convection at correct times, locations, and intensities. Here, realistic convective diabatic heating, learned from full-physics convection-permitting Weather Research and Forecasting simulations, is predicted from weather radar observations using neural networks and a previously developed look-up table.
Bayesian History Matching Applied to the Calibration of a Gravity Wave Parameterization
Authors:
Robert King, Laura Mansfield, and Aditi Sheshadri
Abstract:
Breaking atmospheric gravity waves (GWs) in the tropical stratosphere are essential in driving the roughly 2-year oscillation of zonal winds in this region known as the Quasi-Biennial Oscillation (QBO). As Global Climate Models (GCM)s are not typically able to directly resolve the spectrum of waves required to drive the QBO, parameterizations are necessary. Such parameterizations often require knowledge of poorly constrained physical parameters. In the case of the spectral gravity parameterization used in this work, these parameters are the total equatorial GW stress and the half width of phase speed distribution Radiosonde observations are used to obtain the period and amplitude of the QBO, which are compared against values obtained from a GCM. We utilize two established calibration techniques to obtain estimates of the range of plausible parameter values: History matching & Ensemble Kalman Inversion (EKI).
The role of inertia-gravity waves in the atmospheric energy spectrum: insights from global storm-resolving simulations
Authors:
Yanmichel Morfa Avalos
Abstract:
This dissertation examines the kinetic energy spectra of atmospheric motions, focusing on both horizontal and vertical components using global storm-resolving simulations. Horizontal kinetic energy follows canonical power laws, with a steep 𝜅−3 decline at synoptic scales (∼10,000–1,000 km) driven by quasigeostrophic turbulence, and a shallower 𝜅−5/3 regime at mesoscales (<600 km), though the origins of this mesoscale spectrum remain debated. Vertical kinetic energy spectra, less studied due to measurement challenges, exhibit nearly white spectra with peaks at synoptic and mesoscale ranges, attributed primarily to inertia-gravity wave (IGW) fluctuations.
Overcoming set imbalance in data driven parameterization: A case study of gravity wave momentum transport
Authors:
L. Minah Yang and Edwin P. Gerber
Abstract:
Machine learning for the parameterization of subgrid-scale processes in climate models has been widely researched and adopted in a few models. A key challenge in developing data-driven parameterization schemes is how to properly represent rare, but important events that occur in geoscience datasets. We investigate and develop strategies to reduce errors caused by insufficient sampling in the rare data regime, under constraints of no new data and no further expansion of model complexity. Resampling and importance weighting strategies are constructed with user defined parameters that systematically vary the sampling/weighting rates in a linear fashion and curb too much oversampling.
Explainable Offline-Online Training of Neural Networks for Parameterizations: A 1D Gravity Wave-QBO Testbed in the Small-Data Regime
Authors:
Hamid A. Pahlavan, Pedram Hassanzadeh, and M. Joan Alexander
Abstract:
There are different strategies for training neural networks (NNs) as subgrid-scale parameterizations. Here, we use a 1D model of the quasi-biennial oscillation (QBO) and gravity wave (GW) parameterizations as testbeds. A 12-layer convolutional NN that predicts GW forcings for given wind profiles, when trained offline in a big-data regime (100-year), produces realistic QBOs once coupled to the 1D model.
Atmospheric Gravity Waves: Processes and Parameterization
Authors:
Ulrich Achatz, Joan Alexander, Erich Becker, Hye-Yeong Chun, Andreas Dörnbrack, Laura Holt, Riwal Plougonven, Inna Polichtchouk, Kaoru Sato, Aditi Sheshadri, Claudia Christine Stephan, Annelize van Niekerk, and Corwin J. Wright
Abstract:
Atmospheric predictability from subseasonal to seasonal time scales and climate variability are both influenced critically by gravity waves (GW). The quality of regional and global numerical models relies on thorough understanding of GW dynamics and its interplay with chemistry, precipitation, clouds, and climate across many scales. For the foreseeable future, GWs and many other relevant processes will remain partly unresolved, and models will continue to rely on parameterizations.
Machine Learning for Nonorographic Gravity Waves in a Climate Model
Authors:
Steven Hardiman, Adam Scaife, Annelize Niekerk, Rachel Prudden, Aled Owen, Samantha Adams, Tom Dunstan, Nick Dunstone, and Sam Madge
Abstract:
There is growing use of machine learning algorithms to replicate subgrid parameterization schemes in global climate models. Parameterizations rely on approximations; thus, there is potential for machine learning to aid improvements. In this study, a neural network is used to mimic the behavior of the nonorographic gravity wave scheme used in the Met Office climate model, important for stratospheric climate and variability.